글
마할라노비스 거리는 군집분석에서 가장 많이 사용되는 거리개념으로서, 두 지점의 단순한 거리뿐만이 아니라, 변수의 특성을 나타내는 표준편차와 상관계수가 함께 고려된다는 특징을 가지고 있다.
공분산 행렬(Covariance Matrix)은 아래와 같다라고 하자.
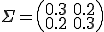
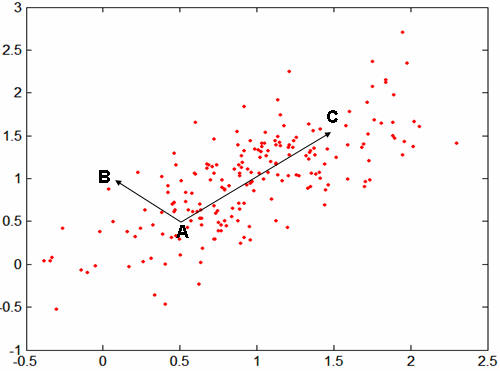
A, B, C 각각의 위치는 다음과 같다.
A(0.5, 0.5)
B(0, 1)
C(1.5, 1.5)
마할라노비스 거리 구하는 공식은 아래와 같다.
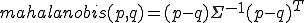
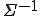 은 공분산 행렬의 역행렬이고,
은 공분산 행렬의 역행렬이고, 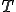 는 변환행렬이다.
는 변환행렬이다.
먼저, 공분산 행렬의 역행렬을 구하자. 2차 정방행렬의 역행렬 구하는 공식은 다음과 같다.
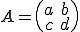 일 때, A의 역행렬
일 때, A의 역행렬 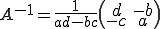 이다.
이다.
위식에 의해 공분산 행렬의 역행렬을 구하면
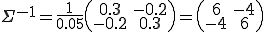 이다.
이다.
마할라노비스 거리 공식에 의해 A,B의 거리와 A,C의 거리를 구해보자.
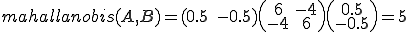
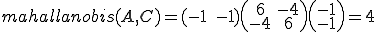
유클리안 거리와 비교해서 결과가 반대로 나왔음을 알 수 있다. 즉, 상관에 따른 거리가 변할 수 있음을 나타낸다
마할라노비스 거리란 각각의 케이스가 여러가지 변인(variables) 중심값 (평균값, mean) 들로 이루어진 중심 (centroid) 에 대해서 갖는 거리를 말한다. 개념적으로 살펴보면, 여러변인을 동시에 이용하여 살펴보는 테스트 (multivariate) 경우에 각각의 중심값을 중앙에 교차시켜 케이스 값들을 나열해보면 일종의 군집을 이루게 되는데, Mahalanobis distance는 특정 케이스의 값이 여기서 심하게 벗어났는가를 보기 위한 거리값이다.
이렇게 얻은 각 case의 값을 데이터로  distribution 을 이용하여 극한 값을 가려낼 수 있는데, 데이터의 극한 값을 찾는데 쓰이기도 한다. 그 판단의 기준은
distribution 을 이용하여 극한 값을 가려낼 수 있는데, 데이터의 극한 값을 찾는데 쓰이기도 한다. 그 판단의 기준은  값의 p 가치가 .001보다 작을 때 (즉, standard deviation 거리의 약 3-4배가 넘을 때) 이다.
값의 p 가치가 .001보다 작을 때 (즉, standard deviation 거리의 약 3-4배가 넘을 때) 이다.
군집분석을 실시하는 경우 대부분 군집분석을 실시하기 전 모들 변수들을 평균 0, 분산 1의 변환된 변수로 표준화 시킨다.
 distribution 을 이용하여 극한 값을 가려낼 수 있는데, 데이터의 극한 값을 찾는데 쓰이기도 한다. 그 판단의 기준은
distribution 을 이용하여 극한 값을 가려낼 수 있는데, 데이터의 극한 값을 찾는데 쓰이기도 한다. 그 판단의 기준은  값의 p 가치가 .001보다 작을 때 (즉, standard deviation 거리의 약 3-4배가 넘을 때) 이다.
값의 p 가치가 .001보다 작을 때 (즉, standard deviation 거리의 약 3-4배가 넘을 때) 이다. 군집분석을 실시하는 경우 대부분 군집분석을 실시하기 전 모들 변수들을 평균 0, 분산 1의 변환된 변수로 표준화 시킨다.
아래 그림과 같은 점 A,B,C 가 있다고 하자.
공분산 행렬(Covariance Matrix)은 아래와 같다라고 하자.
A, B, C 각각의 위치는 다음과 같다.
A(0.5, 0.5)
B(0, 1)
C(1.5, 1.5)
마할라노비스 거리 구하는 공식은 아래와 같다.
먼저, 공분산 행렬의 역행렬을 구하자. 2차 정방행렬의 역행렬 구하는 공식은 다음과 같다.
위식에 의해 공분산 행렬의 역행렬을 구하면
마할라노비스 거리 공식에 의해 A,B의 거리와 A,C의 거리를 구해보자.
유클리안 거리와 비교해서 결과가 반대로 나왔음을 알 수 있다. 즉, 상관에 따른 거리가 변할 수 있음을 나타낸다
[출처] 마할라노비스 (Mahalanobis) 거리 구하기 예제|작성자 다니엘

RECENT COMMENT