Written by Vincent
Image rotation with bilinear interpolation
In this article, I’ll show you how to rotate an image about its centre. 3 assignment methods will be shown,
- assign source pixels to destination pixels
- assign destination pixels from source pixels
- assign destination pixels from source pixels with bilinear interpolation
I’ll show you the code, then the results for comparison. So what’s bilinear interpolation?
Bilinear interpolation
Read up on linear interpolation first if you haven’t done so. “Bilinear” means there are 2 directions to interpolate. Let me illustrate.

In our case, we’re interpolating between 4 pixels. Visualise each pixel as a single point. Linearly interpolate between the top 2 pixels. Linearly interpolate between the bottom 2 pixels. Then linearly interpolate between the calculated results of the previous two.
You can expand on this concept to get trilinear interpolation.

LERPs is a short form of linear interpolations. When would trilinear interpolation be useful? Voxels, which is out of scope in this article.
Defining the centre of an image
I’m going to be fuzzy about this. I’m going to just take one pixel in the image and define it as the centre. This pixel is defined as having a horizontal index equal to half of its width (rounded down), and a vertical index equal to half its height (rounded down).
This means the image isn’t rotated about its “true” centre, but with a relatively large size, it won’t matter anyway. It’s not like you’re rotating an image of 5 pixel width and 3 pixel height, right?
The preparation part
The actual code is quite long, so I’m separating it into 4 parts.
- Initialisation and variable declaration
- Assigning source pixels to destination pixels
- Assigning destination pixels from source pixels
- Assigning destination pixels from source pixels with bilinear interpolation
It’s hard-coded with -30 degrees as the angle of rotation, but you can easily write it into a function.
// 30 deg = PI/6 rad
// rotating clockwise, so it's negative relative to Cartesian quadrants
const double cnAngle = -0.52359877559829887307710723054658;
// use whatever image you fancy
Bitmap bm = new Bitmap("rotationsource.jpg");
// general iterators
int i, j;
// calculated indices in Cartesian coordinates
int x, y;
double fDistance, fPolarAngle;
// for use in neighbouring indices in Cartesian coordinates
int iFloorX, iCeilingX, iFloorY, iCeilingY;
// calculated indices in Cartesian coordinates with trailing decimals
double fTrueX, fTrueY;
// for interpolation
double fDeltaX, fDeltaY;
// pixel colours
Color clrTopLeft, clrTopRight, clrBottomLeft, clrBottomRight;
// interpolated "top" pixels
double fTopRed, fTopGreen, fTopBlue;
// interpolated "bottom" pixels
double fBottomRed, fBottomGreen, fBottomBlue;
// final interpolated colour components
int iRed, iGreen, iBlue;
int iCentreX, iCentreY;
int iWidth, iHeight;
iWidth = bm.Width;
iHeight = bm.Height;
iCentreX = iWidth / 2;
iCentreY = iHeight / 2;
Bitmap bmSourceToDestination = new Bitmap(iWidth, iHeight);
Bitmap bmDestinationFromSource = new Bitmap(iWidth, iHeight);
Bitmap bmBilinearInterpolation = new Bitmap(iWidth, iHeight);
for (i = 0; i < iHeight; ++i)
{
for (j = 0; j < iWidth; ++j)
{
// initialise when "throwing" values
bmSourceToDestination.SetPixel(j, i, Color.Black);
// since we're looping, we might as well do for the others
bmDestinationFromSource.SetPixel(j, i, Color.Black);
bmBilinearInterpolation.SetPixel(j, i, Color.Black);
}
}
Some of it might not mean anything to you yet. Just wait for the rest of the code. You might want to read up on converting between raster, Cartesian and polar coordinates first before moving on.
Throwing values from source to destination
// assigning pixels from source image to destination image
for (i = 0; i < iHeight; ++i)
{
for (j = 0; j < iWidth; ++j)
{
// convert raster to Cartesian
x = j - iCentreX;
y = iCentreY - i;
// convert Cartesian to polar
fDistance = Math.Sqrt(x * x + y * y);
fPolarAngle = 0.0;
if (x == 0)
{
if (y == 0)
{
// centre of image, no rotation needed
bmSourceToDestination.SetPixel(j, i, bm.GetPixel(j, i));
continue;
}
else if (y < 0)
{
fPolarAngle = 1.5 * Math.PI;
}
else
{
fPolarAngle = 0.5 * Math.PI;
}
}
else
{
fPolarAngle = Math.Atan2((double)y, (double)x);
}
// the crucial rotation part
fPolarAngle += cnAngle;
// convert polar to Cartesian
x = (int)(Math.Round(fDistance * Math.Cos(fPolarAngle)));
y = (int)(Math.Round(fDistance * Math.Sin(fPolarAngle)));
// convert Cartesian to raster
x = x + iCentreX;
y = iCentreY - y;
// check bounds
if (x < 0 || x >= iWidth || y < 0 || y >= iHeight) continue;
bmSourceToDestination.SetPixel(x, y, bm.GetPixel(j, i));
}
}
bmSourceToDestination.Save("rotationsrctodest.jpg", System.Drawing.Imaging.ImageFormat.Jpeg);
It should be fairly easy to read. Note the part about checking for the central pixel of the image. No rotation calculation necessary, so we assign and move to the next pixel. Note also the part about checking boundaries.
Finding values from the source
// assigning pixels of destination image from source image
for (i = 0; i < iHeight; ++i)
{
for (j = 0; j < iWidth; ++j)
{
// convert raster to Cartesian
x = j - iCentreX;
y = iCentreY - i;
// convert Cartesian to polar
fDistance = Math.Sqrt(x * x + y * y);
fPolarAngle = 0.0;
if (x == 0)
{
if (y == 0)
{
// centre of image, no rotation needed
bmDestinationFromSource.SetPixel(j, i, bm.GetPixel(j, i));
continue;
}
else if (y < 0)
{
fPolarAngle = 1.5 * Math.PI;
}
else
{
fPolarAngle = 0.5 * Math.PI;
}
}
else
{
fPolarAngle = Math.Atan2((double)y, (double)x);
}
// the crucial rotation part
// "reverse" rotate, so minus instead of plus
fPolarAngle -= cnAngle;
// convert polar to Cartesian
x = (int)(Math.Round(fDistance * Math.Cos(fPolarAngle)));
y = (int)(Math.Round(fDistance * Math.Sin(fPolarAngle)));
// convert Cartesian to raster
x = x + iCentreX;
y = iCentreY - y;
// check bounds
if (x < 0 || x >= iWidth || y < 0 || y >= iHeight) continue;
bmDestinationFromSource.SetPixel(j, i, bm.GetPixel(x, y));
}
}
bmDestinationFromSource.Save("rotationdestfromsrc.jpg", System.Drawing.Imaging.ImageFormat.Jpeg);
The key difference here is the use of the rotation angle. Instead of adding it, we subtract it. The reason is, we rotate source pixels 30 degrees clockwise and assign it to destination pixels. But from destination pixels, we get source pixels which are rotated 30 degrees anticlockwise. Either way, we get a destination image that's the source image rotated 30 degrees clockwise.

Also compare the assignment, noting the indices:
bmSourceToDestination.SetPixel(x, y, bm.GetPixel(j, i));
bmDestinationFromSource.SetPixel(j, i, bm.GetPixel(x, y));
x and y variables are calculated and thus "messy". I prefer my messy indices on the right. There's a practical reason for it too, which will be evident when I show you the rotation results.
Image rotation code with bilinear interpolation
// assigning pixels of destination image from source image
// with bilinear interpolation
for (i = 0; i < iHeight; ++i)
{
for (j = 0; j < iWidth; ++j)
{
// convert raster to Cartesian
x = j - iCentreX;
y = iCentreY - i;
// convert Cartesian to polar
fDistance = Math.Sqrt(x * x + y * y);
fPolarAngle = 0.0;
if (x == 0)
{
if (y == 0)
{
// centre of image, no rotation needed
bmBilinearInterpolation.SetPixel(j, i, bm.GetPixel(j, i));
continue;
}
else if (y < 0)
{
fPolarAngle = 1.5 * Math.PI;
}
else
{
fPolarAngle = 0.5 * Math.PI;
}
}
else
{
fPolarAngle = Math.Atan2((double)y, (double)x);
}
// the crucial rotation part
// "reverse" rotate, so minus instead of plus
fPolarAngle -= cnAngle;
// convert polar to Cartesian
fTrueX = fDistance * Math.Cos(fPolarAngle);
fTrueY = fDistance * Math.Sin(fPolarAngle);
// convert Cartesian to raster
fTrueX = fTrueX + (double)iCentreX;
fTrueY = (double)iCentreY - fTrueY;
iFloorX = (int)(Math.Floor(fTrueX));
iFloorY = (int)(Math.Floor(fTrueY));
iCeilingX = (int)(Math.Ceiling(fTrueX));
iCeilingY = (int)(Math.Ceiling(fTrueY));
// check bounds
if (iFloorX < 0 || iCeilingX < 0 || iFloorX >= iWidth || iCeilingX >= iWidth || iFloorY < 0 || iCeilingY < 0 || iFloorY >= iHeight || iCeilingY >= iHeight) continue;
fDeltaX = fTrueX - (double)iFloorX;
fDeltaY = fTrueY - (double)iFloorY;
clrTopLeft = bm.GetPixel(iFloorX, iFloorY);
clrTopRight = bm.GetPixel(iCeilingX, iFloorY);
clrBottomLeft = bm.GetPixel(iFloorX, iCeilingY);
clrBottomRight = bm.GetPixel(iCeilingX, iCeilingY);
// linearly interpolate horizontally between top neighbours
fTopRed = (1 - fDeltaX) * clrTopLeft.R + fDeltaX * clrTopRight.R;
fTopGreen = (1 - fDeltaX) * clrTopLeft.G + fDeltaX * clrTopRight.G;
fTopBlue = (1 - fDeltaX) * clrTopLeft.B + fDeltaX * clrTopRight.B;
// linearly interpolate horizontally between bottom neighbours
fBottomRed = (1 - fDeltaX) * clrBottomLeft.R + fDeltaX * clrBottomRight.R;
fBottomGreen = (1 - fDeltaX) * clrBottomLeft.G + fDeltaX * clrBottomRight.G;
fBottomBlue = (1 - fDeltaX) * clrBottomLeft.B + fDeltaX * clrBottomRight.B;
// linearly interpolate vertically between top and bottom interpolated results
iRed = (int)(Math.Round((1 - fDeltaY) * fTopRed + fDeltaY * fBottomRed));
iGreen = (int)(Math.Round((1 - fDeltaY) * fTopGreen + fDeltaY * fBottomGreen));
iBlue = (int)(Math.Round((1 - fDeltaY) * fTopBlue + fDeltaY * fBottomBlue));
// make sure colour values are valid
if (iRed < 0) iRed = 0;
if (iRed > 255) iRed = 255;
if (iGreen < 0) iGreen = 0;
if (iGreen > 255) iGreen = 255;
if (iBlue < 0) iBlue = 0;
if (iBlue > 255) iBlue = 255;
bmBilinearInterpolation.SetPixel(j, i, Color.FromArgb(iRed, iGreen, iBlue));
}
}
bmBilinearInterpolation.Save("rotationbilinearinterpolation.jpg", System.Drawing.Imaging.ImageFormat.Jpeg);
This part is similar to the destination-from-source part, with a lot more calculations. We have to find the 4 pixels that surrounds our "true" position-calculated pixel. Then we perform linear interpolation on the 4 neighbouring pixels.
We need to interpolate for the red, green and blue components individually. Refer to my article on colour theory for a refresher.
Pictures, pictures!
After doing all that, we're finally done. Let me show you my source image first.

I added the marble cylinder for emphasising image quality. I needed something that's straight (vertically or horizontally) in the source image.
Here's what we get after rotating with the source-to-destination method:

Note the speckled black pixels dotted all over. This is because some of the destination pixels (which are within the image bounds) were unassigned.
Note also that the specks even form patterns. This is due to the sine and cosine functions, and the regularity of pixel width and height. Sine and cosine are periodic functions. Since pixel indices are regular, therefore sine and cosine results are regular too. Hence, calculations regularly fail to assign pixel values.
There might be source pixels that have the same calculated destination pixel (due to sine and cosine and rounding). This also implies that there might be anti-gravity destination pixels that no source pixel can ever matched to! I haven't verified this, but it seems a possibility.

Still think you should iterate over the source (image/array) instead of over the destination?
Next, we have the image result of the destination-from-source method:

Compare the quality with the source-to-destination part. No missing pixels. It's still sort of grainy though. This is because some of the destination pixels get their values from the same source pixel, so there might be 2 side-by-side destination pixels with the same colour. This gives mini blocks of identical colour in the result, which on the whole, gives an unpolished look.
Now, we have the bilinear interpolation incorporated version.

It looks smoother, right? Note the straight edge of the marble cylinder. Compare with the image result without bilinear interpolation.
I might do a version with cubic interpolation for even smoother results, but I feel the bilinear version is good enough for now. Have fun!
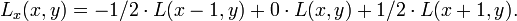















RECENT COMMENT