Markov Process, Markov Chain

마르코프 프로세스(Markov Process) 정의
  ㅇ 어떤 상태로 들어갈 확률이 들어가기 직전 상태에 만 의존하는 확률과정(랜덤 과정)을 의미함
    즉, 다음에 나올 상태에 대한 확률 값이 바로 직전의 과거에만 종속되어있으며 그 이전 과거의
    정보와 무관한 프로세스(Memoryless Process)    

  ㅇ 마르코프 프로세스의 예
    일반적으로 문장 내에 연이어 나올 글자,구절들은 이전 글자, 구절과 상관성을 갖게되므로 이를 
    메모리(기억성) 요소가 있다고 한다(Memory Process)
    또한 신호가 주파수 스펙트럼 상에서 특정 주파수대에 몰려있으면, 이 신호는 시간적 상관성을 
    가진다고 볼 수 있므로 해당 신호는 모두 메모리를 가지고 있다고 말할 수 있음
 
마르코프 체인(Markov Chain) 정의
  ㅇ 마르코프 프로세스에서 연속적인 시간변화를 고려 않고, 이산적인 경우 만 고려한 반복천이 과정

  ㅇ 마르코프 체인의 특징
     - 각 시행의 결과가 여러개의 미리 정해진 결과 중의 하나가 됨
     - 각 시행의 결과는 바로 직전 시행의 결과에 만 영향 받음

  ㅇ 마르코프 연쇄의 식 표현
     - 일정 시간 간격 (상태) 마다 반복 천이되며, 천이확률이 매 천이 마다 동일함
        . 이러한 연쇄(Chain)를 설명하는 확률 행렬을 확률 천이 행렬이라고 함
       
        .  x(k) : 상태벡터(State Vector)
        .  pij   : 천이확률(Transition Probability)
        .  P    : 천이행렬/확률행렬(Transition Matrix/Probability Matrix)

     - 임의 시각의 상태까지 반복적으로 계산할 수 있음
       
 
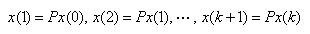
        . 즉, 천이확률과 초기 상태벡터에 의해 완전히 결정됨
 
<정보통신 기술용어해설 > 에서 발췌 정리