글
From Wikipedia, the free encyclopedia
Empirical risk minimization (ERM) is a principle in statistical learning theory which defines a family of learning algorithms and is used to give theoretical bounds on the performance of learning algorithms.
Background
Consider the following situation, which is a general setting of many supervised learning problems. We have two spaces of objects X and Y and would like to learn a function 
(often called hypothesis) which outputs an object 
, given 
. To do so, we have in our disposal a training set of a few examples 
where 
is an input and 
is the corresponding response that we wish to get from 
.
To put it more formally, we assume that there is a joint probability distribution P(x,y) over X and Y, and that the training set consists of m instances drawn i.i.d. from P(x,y). Note that the assumption of a joint probability distribution allows us to model uncertainty in predictions (e.g. from noise in data) because y is not a deterministic function of x, but rather a random variable with conditional distribution P(y | x) for a fixed x.
We also assume that we are given a non-negative real-valued loss function 
which measures how different is the prediction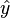 
of a hypothesis from the true outcome y. The risk associated with hypothesis h(x) is then defined as the expectation of the loss function:
![R(h) = \mathbf{E}[L(h(x), y)] = \int L(h(x), y)\,dP(x, y).](http://upload.wikimedia.org/math/f/c/5/fc5a0829e5d2623238d89a47fcf2a701.png)
A loss function commonly used in theory is the 0-1 loss function: 
, where I(...) is the indicator notation.
The ultimate goal of a learning algorithm is to find a hypothesis 
among a fixed class of functions 
for which the risk R(h) is minimal:
Empirical risk minimization
In general, the risk R(h) cannot be computed because the distribution P(x,y) is unknown to the learning algorithm (this situation is referred to as agnostic learning). However, we can compute an approximation, called empirical risk, by averaging the loss function on the training set:
Empirical risk minimization principle states that the learning algorithm should choose a hypothesis 
which minimizes the empirical risk:
Thus the learning algorithm defined by ERM principle consists in solving the above optimization problem.
RECENT COMMENT