1. 유사도 정의
군집 분석에서 상사성이 높은 개체(유전자 혹은 환자)들은 같은 군집(발현 양상이 비슷한 유전자들 혹은 같은 종류의 암 환자)에 포함시키고, 상대적 상사성이 낮은 개체(발현 양상이 다르거나 다른 종류의 암 환자)들은 서로 다른 군집에 포함시킬 수 있도록 해주는 상사성이나 비상사성을 측정하는 유사도 정의가 필요 한다. 이러한 유사도 정의에 주로 사용되는 것은 거리인데 대표적으로 사용되는 거리 척도에는 Euclidean 거리이다.

한편 Euclidean 거리는 사용된 척도에 따라서 거리 순위에 상당한 영향을 미치게 된다. 이러한 문제를 극복하기 위하여 일반적으로 각 변수를 표준 편차로 나눈 표준화 변수를 사용하게 된다. 그러나 변수들 사이의 상관관계가 존재 할 때 거리는 척도의 불변성과 상관관계를 고려한 통계적 거리로 측정되어야 한다. 이러한 통계적 거리를
Mahalanobis 거리라고 한다.
한편 Euclidean 거리 이외에 개체들 간의 유사도 평가 기준으로는 pearson correlation coefficient, spearman correlation coefficient나 mutual information이 사용되기도 한다. 유사도에 대한 정의를 어떻게 했느냐가 군집의 질에 영향을 미치게 된다.
2. 계보적 군집 방법
계보적 군집 방법에는 상사성이 밀접한 개체(유전자나 암 환자)들을 단계적으로 발현 양상이 비슷한 유전자들이나 같은 종류의 암 환자들로 이루어진 군집을 형성해 나가는 병합적 방법 (agglomerative method)이 많이 사용 된다. 병합적 방법에서는 각 개체가 별개 군집을 형성하기 때문에 n개 군집에서 출발한다. 연속되는 각 단계 마다 가까운 두 개 군집들을 병합하면, 각 단계 마다 군집의 수가 하나씩 줄어든다. 따라서 마지막 단계에서는 모든 개체들이 하나의 군집을 형성하게 된다. 이러한 계보적 방법에 의한 군집 형성 결과는 이차원상의 도면에 나타낸 dendrogram 형식으로 표시될 수 있다 (그림 1).
병합적 방법으로는 두 군집 사이의 거리에 대한 정의 방법에 따라 군집 연결 방법이 달라지는데 최단 연결법, 최장 연결법, 평균 연결법, 중심 연결법 등이 있다. 최단 연결법은 우선 (NxN) 거리 행렬 D에서 우선 거리가 가장 가까운 개체가 U, V라면 두 개체를 묶어서 군집 (U V)를 형성한다. 다음 단계는 군집 (U V)와 나머지 (N-2)개의 다른 개체 중 임의의 개체 W와의 최소 거리를 다음과 같이 계산한 후
()min{,}UVWuwvwdd d =
거리 행렬에서 거리가 가장 가까운 개체와 다시 군집을 형성한다. 이러한 과정을 반복 하면 모든 개체를 포함하는 하나의 군집을 형성하게 된다.
최장 연결법은 우선 (NxN) 거리 행렬 D에서 우선 거리가 가장 가까운 개체가 U, V라면 두 개체를 묶어서 군집 (U V)를 형성한다. 다음 단계는 군집 (U V)와 나머지 (N-2)개의 다른 개체 중 임의의 개체 W와의 최대 거리를 다음과 같이 계산한 후
()max{,}UVWuwvwdd d =
거리 행렬에서 거리가 가장 가까운 개체와 다시 군집을 형성한다. 이러한 과정을 반복 하면 모든 개체를 포함하는 하나의 군집을 형성하게 된다.
평균 연결법은 우선 (NxN) 거리 행렬 D에서 우선 거리가 가장 가까운 개체가 U, V라면 두 개체를 묶어서 군집 (U V)를 형성한다. 다음 단계는 군집 (U V)와 나머지 (N-2)개의 다른 개체 중 임의의 개체 W와의 평균 거리를 다음과 같이 계산한 후 ()()ijijUVWuvwddnn=ΣΣ
거리 행렬에서 거리가 가장 가까운 개체와 다시 군집을 형성한다. 이러한 과정을 반복 하면 모든 개체를 포함하는 하나의 군집을 형성하게 된다.
중심 연결법은 두 군집 사이의 거리는 두 군집의 중심간의 거리로 계산 된다. 만약 군집 C1에 속하는 개체의 수가 N1 일 때 군집 C1의 중심은 11iiicXXn∈=Σ
이 된다. 군집 C2에 속하는 N2개체의 중심을 2X라고 하면 두 군집 사이의 거리는 122()()1212(,)CCdPXXX==−X
이 된다. 여기서 P는 근접 척도로 Euclidean 거리의 자승이 사용된다. 만약 두 군집이 결합되면 새로운 군집의 중심은 가중 평균을 이용하여 구하고 각 군집 사이의 거리를 구한후 중심 거리가 가장 가까운 개체와 다시 새로운 군집을 형성한다. 이러한 과정을 반복하면 모든 개체를 포함하는 하나의 군집을 형성하게 된다.
평균을 이용하여 구하고 각 군집 사이의 거리를 구한후 중심 거리가 가장 가까운 개체와 다시 새로운 군집을 형성한다. 이러한 과정을 반복하면 모든 개체를 포함하는 하나의 군집을 형성하게 된다.
3. 분리 군집 방법
계보적 군집 방법에서는 일단 어떤 개체가 특정한 군집에 할당되면 다른 군집에 다시 할당 될 수 없는 단점을 가지고 있다. 반면에 분리 군집 방법은 어떤 개체가 초기 할당에서 잘못 되었다 하더라도 다시 할당할 수 있는 방법이다. 이 분리 군집 방법은 미리 설정된 기준의 최적화에 근거해서 자료를 분리하게 된다. 또한 이 방법을 사용할 때에는 최종 군집의 수가 알려져 있고 또한 미리 설정될 수 있다고 가정한다.
분리군집 방법으로 가장 대표적인 k-평균 군집 방법은 다음과 같다. n개 개체(유전자나 암 환자)가 p차원 다변량 개체라고 했을 때 각 개체는 초기에 설정된 k개의 발현 양상이 비슷한 유전자들이나 같은 종류의 암 환자들로 이루어진 군집중 어느 한 군집에 할당된다고 가정하자. 이때 i번째 개체의 j번째 변수를 X(i,j)로 표시하고, c번째 군집에 속한 nc개 개체들의 j번째 변수에 대한 평균을 X(c,j)로 표시했을 때 i번째 개체와 c번째 군집 사이의 Euclidean 거리는 다음과 같이 표시 할 수 있다. 0.521(,)(,)(,)pjDicXijXcj==−Σ
또한 각 개체를 c번째 군집에 재 할당할 때 오차 자승 합 E는
[]21(,())niEDici==Σ
이 된다. 위 식에서 c(i)는 군집 c는 i번째 개체를 포함하고 있다는 것이고, D(i,c(i))는 i번째 개체와 그 개체를 포함하고 있는 군집 사이의 Euclidean 거리를 표시한다. 따라서 분리 군집 방법은 각 개체를 어느 한 군집으로부터 다른 군집으로 움직일 때 오차 자승 합을 계산하여 비교하면서 더 이상 움직일 개체가 없을 때인 오차 자승 합이 최소화 하는 곳까지 반복한다.
4. 최근 제안 되는 군집화 방법
최근 들어 많은 전산학자와 통계 학자, 생물학자들이 개인 별로 또는 팀을 형성하여 군집화 방법을 개발하고 있으며 논문들이 발표되고 있다. 대표적인 논문들에 대해서 아래의 표에 설명 했다.
논문
발표 년도 사용 기법
실험 데이터
소프트 웨어
비고
Eisen et al
1998
계층적 군집화 분석
budding yeast cell cycle
공개
Cluster와 TreeView 프로그램
Tamayo et al
1999
SOM(self organizing map)
Budding yeast cell cycle
공개
Tavazoie et al
1999
K 평균 군집화 분석
budding yeast cell cycle
공개
Ben-Dor et al
1999
CAST
공개
Biocluster 프로그램
Sharan et al
2000
CLICK
Budding yeast cell cycle
라이센스 등록후 제공
계층적 군집화 분석과 비교 결과 제시
표 1 연구 동향
Eisen등은 통계학에서 널리 쓰이는 계층적 군집화를 DNA microarray에 적용하여 좋은 연구 업적을 남겼고, 이 연구의 산출물인 Cluster 와 TreeView라는 소프트웨어는 많은 사람에 의해 사용되고 있다. 이외에도 Hartuv는 그래프 이론을 바탕으로 군집화 방법을 제안하였고. Ben-Dor와 Shamir등도 역시 그래프를 응용하여 CAST라는 방법을 제안하고 프로그램으로 구현하였다. Tamayo등은 SOM(self –organizing maps)라는 방법을 적용하였으며 이외의 다수가 현재 군집화 방법의 개발 또는 평가 논문을 제시하고 있다.
5. 군집 분석시 유의 사항
군집을 형성하는 방법에는 여러 방법이 있지만 최적 방법에 대한 기준은 명확하지 않다. 따라서 군집 분석을 할 때 유의해야 할 사항을 정리하면 다음과 같다.
하나. 만약 집단들 사이에 상당한 차이가 없다면 현실적으로 군집 분석에서 매우 명확한 결과를 기대할 수 없을 것이다. 특히 만약 개체들이 비선형 형태로 분포되어 있다면 명확한 군집들을 찾아내는 것은 어려울 것이다.
둘. 군집 분석은 이상치에 대하여 상당히 민감한 결과를 보인다. 따라서 군집 분석을 시행하기 전에 자료에 대하여 이상치 존재 여부를 살펴야 한다고 판단된다.
셋, 군집 분석에 사용될 변수들의 측정 척도가 서로 다른 경우에는 분석 전에 표준화하여야 한다.
넷, 군집의 타당성을 검토하기 위하여 두 가지 방법이 사용된다. 첫 번째 방법은 자료에 대하여 여러 가지 군집 방법을 적용한 후 그 결과들이 유사한가를 검토하는 방법이다. 두 번째 방법은 자료를 랜덤 하게 이등분하고 각각에 대하여 여러 가지 군집 방법을 실시한 후 두 개의 결과가 유사한지 여부를 검토하여 일치도가 높은 군집 방법을 선택하는 방법이다.
3. 요약 및 연구 전망
DNA microarray 실험의 일반화와 유전자를 이용한 연구의 발전으로 인하여 데이터들은 급속히 증가되고 있다. 이러한 방대한 양의 정보들을 바탕으로 의미 있는 정보를 획득하는
데 있어서는 군집화 분석이 중요한 위치를 차지하고 있다. 그래프 이론에서의 접근, 신경망을 이용한 학습 기법에서의 접근, 확률 통계학적인 접근 방식으로 여러 군집화 분석이 연구되어 왔다. 특히 계층적 군집화와 분리 군집화 분석의 경우는 단순하면서도 어느 정도 의미 있는 결과를 도출하는 알고리즘으로써 많이 활용되고 있으며 CLICK과 CLIFF는 군집화의 정확성을 더욱 높이는 결과를 가져왔다.
이 분야에 있어서 연구는 지속적인 발전이 있으리라고 본다. 생물학이라는 특수 영역에 의존된 데이터라는 특색과 유전 자수에 비해 실험 횟수는 매우 적은 특수한 환경 제약이 있기 때문에 이를 극복하기 위한 여러 가지 heuristic한 방법들이 계속해서 연구되리라고 전망된다.












 distribution 을 이용하여 극한 값을 가려낼 수 있는데, 데이터의 극한 값을 찾는데 쓰이기도 한다. 그 판단의 기준은
distribution 을 이용하여 극한 값을 가려낼 수 있는데, 데이터의 극한 값을 찾는데 쓰이기도 한다. 그 판단의 기준은 

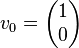

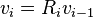
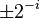 the multiplication with the tangent can be replaced by a division by a power of two, which is efficiently done in digital computer hardware using a
the multiplication with the tangent can be replaced by a division by a power of two, which is efficiently done in digital computer hardware using a 
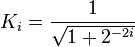

RECENT COMMENT